Abstract

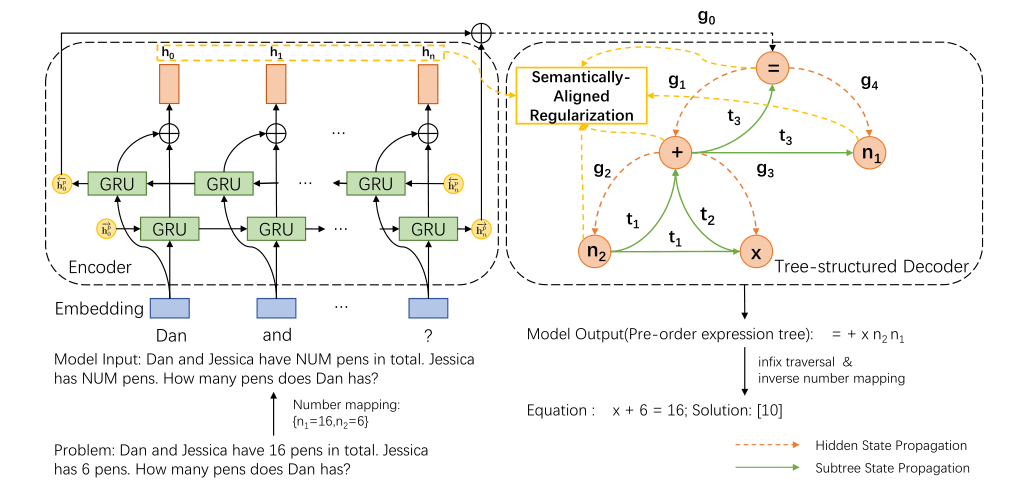
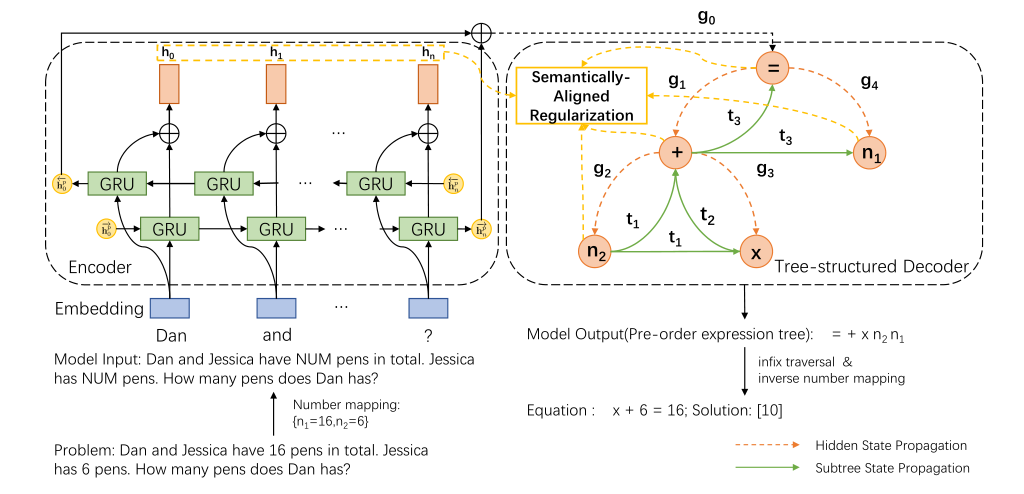
A practical automatic textual math word problems (MWPs) solver should be able to solve various textual MWPs while most existing works only focused on one-unknown linear MWPs. Herein, we propose a simple but efficient method called Universal Expression Tree (UET) to make the first attempt to represent the equations of various MWPs uniformly. Then a semantically-aligned universal tree-structured solver (SAU-Solver) based on an encoder-decoder framework is proposed to resolve multiple types of MWPs in a unified model, benefiting from our UET representation. Our SAU-Solver generates a universal expression tree explicitly by deciding which symbol to generate according to the generated symbols’ semantic meanings like human solving MWPs. Besides, our SAU-Solver also includes a novel subtree-level semanticallyaligned regularization to further enforce the semantic constraints and rationality of the generated expression tree by aligning with the contextual information. Finally, to validate the universality of our solver and extend the research boundary of MWPs, we introduce a new challenging Hybrid Math Word Problems dataset (HMWP), consisting of three types of MWPs. Experimental results on several MWPs datasets show that our model can solve universal types of MWPs and outperforms several state-of-the-art models .

Framework

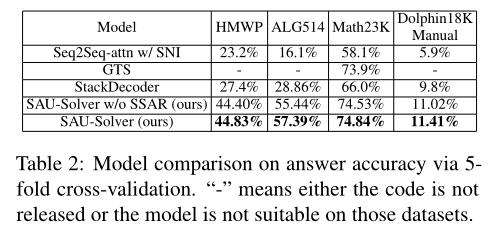
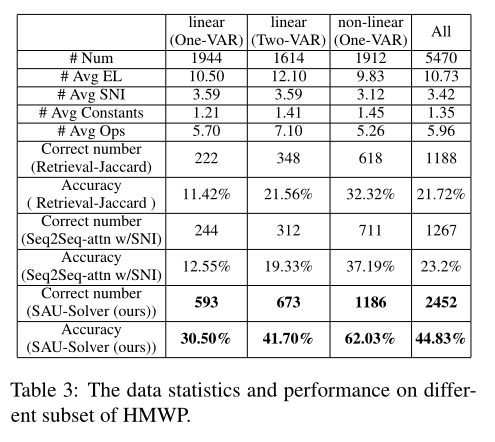
Experiment

Conclusion

We propose an SAU-Solver, which is able to solve multiple types of MWPs, to generate the universal express tree explicitly in a semantically-aligned manner. Besides, we also propose a subtree-level semantically-aligned regularization to improve subtree semantic representation. Finally, we introduce a new MWPs datasets, called HMWP, to validate our solver’s universality and push the research boundary of MWPs to math real-world applications better. Experimental results show the superiority of our approach.