Abstract

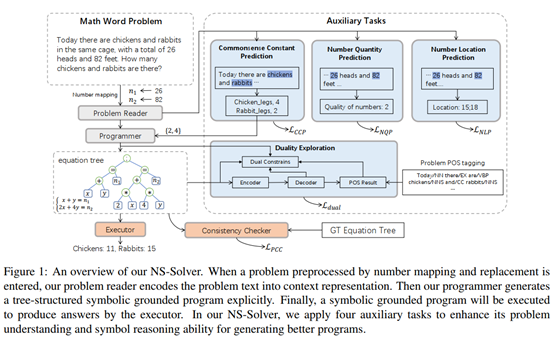
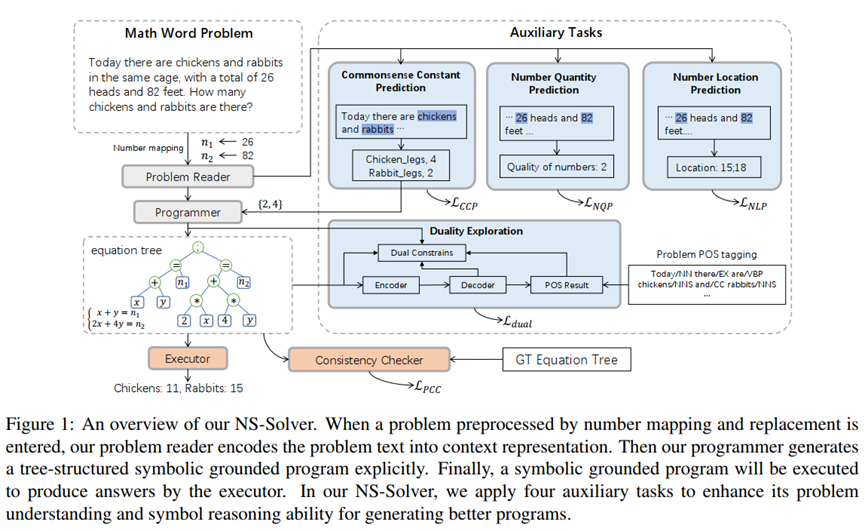
Previous math word problem solvers following the encoder-decoder paradigm fail to explicitly incorporate essential math symbolic constraints, leading to unexplainable and unreasonable predictions. Herein, we propose Neural-Symbolic Solver (NS-Solver) to explicitly and seamlessly incorporate different levels of symbolic constraints by auxiliary tasks. Our NS-Solver consists of a problem reader to encode problems, a programmer to generate symbolic equations, and a symbolic executor to obtain answers. Along with target expression supervision, our solver is also optimized via 4 new auxiliary objectives to enforce different symbolic reasoning: a) self-supervised number prediction task predicting both number quantity and number locations; b) commonsense constant prediction task predicting what prior knowledge (e.g. how many legs a chicken has) is required; c) program consistency checker computing the semantic loss between predicted equation and target equation to ensure reasonable equation mapping; d) duality exploiting task exploiting the quasiduality between symbolic equation generation and problem’s part-of-speech generation to enhance the understanding ability of a solver. Besides, to provide a more realistic and challenging benchmark for developing a universal and scalable solver, we also construct a new largescale MWP benchmark CM17K consisting of 4 kinds of MWPs (arithmetic, one-unknown linear, one-unknown non-linear, equation set) with more than 17K samples. Extensive experiments on Math23K and our CM17k demonstrate the superiority of our NS-Solver compared to state-of-the-art methods.

Framework

Experiment

Conclusion

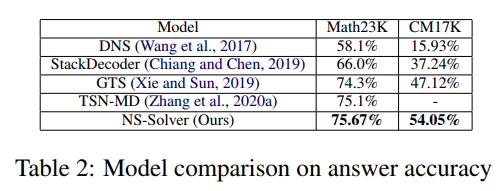
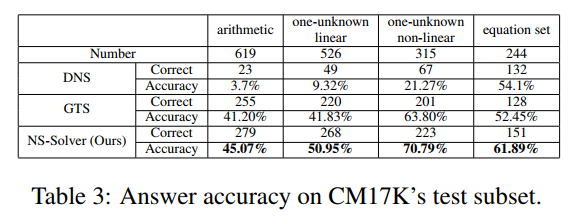
In this work, we propose Neural-Symbolic Solver (NS-Solver) to explicitly and seamlessly incorporate different levels of symbolic constraints by four auxiliary tasks. Our NS-Solver consists of a problem reader to encode problems, a programmer to generate a symbolic grounded program, and a symbolic executor to obtain final results. In addition to supervised learning with target expression, our solver is also optimized via four new auxiliary objectives that enforce four levels of symbolic reasoning. Besides, we also construct a new dataset

CM17K containing 4 types of MWPs with more than 17K samples, which provides a more realistic and challenging benchmark for developing a universal and scalable math solver. Extensive experiments on Math23K and CM17K demonstrate the superiority of our NS-Solver compared to state-of-the-art methods in answer accuracy while ensuring intermediate equation rationality.